Analyseur FT-ICR - Mass-spectrometry

FT-ICR

1. Introduction

Spectromètre de masse FT-ICR Le spectromètre de masse à résonance cyclotronique ionique (FT-ICR) est un instrument de très haute performance, offrant à la fois une résolution exceptionnelle et une précision de mesure de masse extrêmement élevée [1–3]. Grâce à ces caractéristiques, le FT-ICR/MS constitue un outil analytique majeur, largement utilisé en chimie et en chimie des produits naturels, ainsi que dans les sciences de la vie, la biologie et le domaine pharmaceutique.

Le principe de la résonance cyclotronique a été initialement développé par Lawrence et al. en 1930 [4]. Lawrence a conçu le premier accélérateur cyclotronique afin d’étudier les propriétés fondamentales des atomes dans le cadre de la recherche nucléaire. Il a démontré que la fréquence angulaire du mouvement circulaire des particules chargées dans un champ magnétique est indépendante de leur vitesse initiale ainsi que du rayon cyclotronique, mais dépend inversement du rapport masse/charge (m/z) et directement de l’intensité du champ magnétique appliqué.

Quelques années plus tard, Penning a introduit le premier piège permettant de confiner des particules chargées grâce à la combinaison d’un champ électrique statique assurant le piégeage axial et d’un champ magnétique assurant la confinement radial [5]. En 1949, le principe de la résonance cyclotronique des ions a été intégré pour la première fois dans un spectromètre de masse par Hipple et al. [6,7]. Cet instrument, connu sous le nom d’Omegatron, reposait sur l’accélération radiale des ions à leur fréquence cyclotronique, suivie d’une détection sur un collecteur fixe. En raison des limitations technologiques de l’époque, cet appareil présentait toutefois une faible résolution, une gamme de masse restreinte et une utilité analytique limitée.

Par la suite, Wobschall, en collaboration avec la société Varian, a contribué à l’amélioration de la spectrométrie ICR/MS [8]. Le nouvel instrument, appelé Syrotron, intégrait une cellule de type drift divisée en plusieurs régions (source d’ions, analyseur et zone de détection), ainsi qu’un système de détection par oscillateur marginal. Cet instrument a été largement utilisé pour l’étude des réactions ion–molécule en phase gazeuse. Néanmoins, la mesure simultanée de l’ensemble des rapports m/z des ions présents dans la cellule ICR demeurait un défi majeur.

L’introduction du piège ionique ICR [9] a marqué une étape déterminante dans l’évolution de la spectrométrie de masse. Les ions y sont confinés par des électrodes de piégeage soumises à de faibles potentiels électriques, leur permettant de survivre sur de longues durées. Cette avancée a rendu possible une manipulation plus efficace des ions et a conduit à des améliorations significatives en termes de sensibilité, de résolution et de gamme dynamique.

En 1974, la spectrométrie de masse FT-ICR a été décrite pour la première fois par Comisarow et Marshall [10]. Cette avancée a été rendue possible par les progrès de l’informatique, notamment par le développement des convertisseurs analogique–numérique (ADC), permettant la numérisation en temps réel du signal électrique induit par le mouvement cyclotronique des ions dans la cellule ICR. Les signaux temporels ainsi obtenus sont ensuite transformés dans le domaine fréquentiel par application de la transformée de Fourier.

En 1989, McLafferty et al. [11] ont réalisé le couplage d’une source d’ionisation par électrospray (ESI) à un FT-ICR/MS à l’aide d’une injection d’ions via un quadripôle et des étages de pompage différentiel. Cette avancée a considérablement élargi le champ d’application du FT-ICR/MS, notamment à l’analyse de composés non volatils et de macromolécules. Dès lors, les sources d’ionisation externes (ESI, MALDI, LD, auto-ionisation, EI, CI, APCI, APPI, etc.) [11–15] ont progressivement remplacé les sources internes historiquement utilisées.

Parallèlement, les progrès en électronique et en informatique ont permis le développement de diverses méthodes d’excitation (par exemple chirp, SWIFT) ainsi que de modes de détection (broad-band, narrow-band) et de traitements avancés du signal de Fourier, tels que le zero-filling [16] et l’apodisation [17].

De nombreuses modifications de la géométrie des pièges ioniques [18] ont également été proposées afin de minimiser l’influence des potentiels de piégeage sur la fréquence mesurée, dans le but de se rapprocher au maximum de la fréquence cyclotronique théorique des ions.

Les développements majeurs du FT-ICR/MS se sont intensifiés à partir des années 1990, avec l’introduction de champs magnétiques de plus forte intensité [19], l’accumulation d’ions externes [20] et l’intégration de quadripôles externes pour la sélection des ions [21]. En parallèle, plusieurs techniques de dissociation ont été développées et appliquées à la caractérisation des macromolécules, notamment la dissociation induite par collisions (CID [22], SORI-CID [23]), la dissociation multiphotonique infrarouge (IRMPD) [24,25], la capture d’électron (ECD) [26] et le détachement d’électron (EDD) [27].

Aujourd’hui, la spectrométrie de masse FT-ICR/MS est une technique mature et largement utilisée dans de nombreux domaines de recherche, grâce à ses nombreux avantages :

un pouvoir résolutif très élevé (10⁵ à 10⁶ FWHM) ;
une excellente précision de mesure de masse, pouvant atteindre le niveau sub-ppm ;
une grande flexibilité permettant le couplage à de nombreuses sources d’ionisation externes ;
l’accès à plusieurs modes d’activation ionique, dont certains spécifiques aux instruments de piégeage (SORI-CID, IRMPD, ECD, EDD) ;
une haute sensibilité associée à une large gamme dynamique.

2. Principe de base

2.1 Mouvement cyclotronique des ions dans la cellule ICR

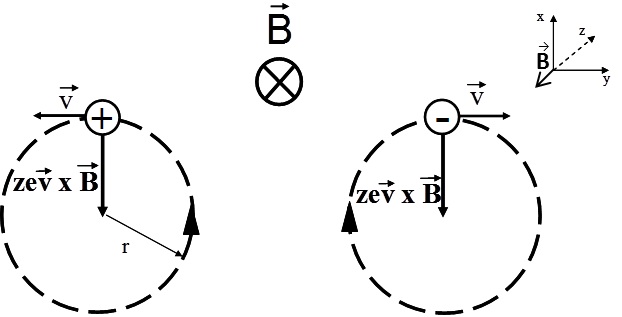
Le principe théorique du FT-ICR/MS repose sur des concepts physiques relativement simples. La trajectoire et le mouvement des ions peuvent être décrits à l’aide d’équations fondamentales. Dans une cellule ICR, les ions sont confinés par un champ magnétique uniforme. Un ion possédant une vitesse initiale v et soumis à un champ magnétique B subit une force de Lorentz (Équation 1), qui induit un mouvement circulaire perpendiculaire à la direction du champ magnétique (Figure 1).

Figure 1: Mouvement cyclotronique des ions positifs et négatifs dans un champ magnétique (modifié à partir de schéma publié par Marshall (79)).

Equation 1, z: nombre de charge

e=1,6.10^-19C

Lorsqu’un ion se déplace dans un champ magnétique uniforme avec une vitesse perpendiculaire au champ, il décrit un mouvement circulaire uniforme de rayon $r$ .

Dans ce cas, la force de Lorentz magnétique exercée sur l’ion est responsable de la courbure de la trajectoire et joue le rôle de force centripète. On a donc l’égalité :

𝐹𝑙𝑜𝑟= Fcen, avec

La fréquence cyclotronique s’exprime ainsi par :

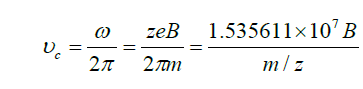
Ce mouvement de rotation est appelé mouvement cyclotronique. Il est caractérisé par une fréquence cyclotronique qui ne dépend que de l’intensité du champ magnétique et du rapport masse sur charge () de l’ion, et est indépendante de sa vitesse initiale.

À partir de cette relation (équation 3), la mesure de la fréquence cyclotronique permet la détermination précise du rapport des ions piégés dans la cellule ICR (Ion Cyclotron Resonance). Il convient de noter que cette fréquence est inversement proportionnelle au rapport : ainsi, un ion possédant un rapport $m / z$ élevé présente une fréquence cyclotronique plus faible.

Bien que les ions ayant le même rapport $m / z$ oscillent à une fréquence cyclotronique identique, le rayon initial de leur trajectoire circulaire peut varier. En effet, ce rayon dépend de la vitesse initiale de l’ion dans le plan , comme l’indique l’équation 4.

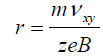équation 4

Piège de Penning

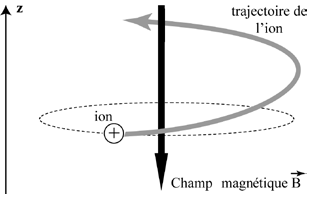
La cellule ICR est un piège de Penning dans lequel les ions sont confinés par la combinaison d’un champ magnétique et d’un champ électrique. Le champ magnétique impose aux ions un mouvement cyclotronique, caractérisé par une trajectoire hélicoïdale infinie le long de l’axe , orienté anti-parallèlement au champ magnétique

. Dans ces conditions, la vitesse angulaire cyclotronique des ions demeure constante (Figure 2).

Afin d’assurer le confinement des ions selon l’axe , deux plaques de piégeage sont placées perpendiculairement au champ magnétique. L’application d’un potentiel électrique crée ainsi un puits de potentiel axial, permettant le stockage des ions à l’intérieur de la cellule. En pratique, un faible potentiel, généralement de l’ordre de 1 V, est appliqué à chacune des plaques de piégeage. Sous l’effet de ce champ électrique, les ions effectuent alors un mouvement oscillatoire axial entre les deux plaques, appelé mouvement de piégeage (Figure 3).

Figure 2 : Mouvement cyclotronique d’un ion dans un champ magnétique

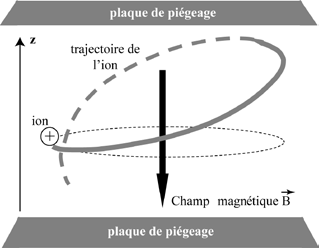
Figure 5 : Mouvement macroscopique d’un ion dans un champ magnétique, piégé entre deux plaques. — Figure 3 : Mouvement macroscopique d’un ion dans un champ magnétique, piégé entre deux plaques.

(Figures adaptés par A. Delvolvé à partir de documentation Bruker.

Dans le cas idéal où le champ électrique appliqué est homogène et parallèle au champ magnétique, et où les plaques de piégeage sont de longueur infinie, le mouvement d’un ion serait strictement hélicoïdal. Dans ces conditions, l’ion effectuerait des oscillations axiales périodiques le long de l’axe au sein du puits de potentiel électrique. La fréquence de piégeage, notée ν_T peut alors être définie par l’équation (5).

En pratique, le champ électrique appliqué ne peut pas être parfaitement parallèle au champ magnétique. Cette non-idéalité engendre une composante radiale du champ électrique, laquelle induit un troisième type de mouvement ionique. Ce mouvement, appelé mouvement magnétron, est caractérisé par une faible fréquence et tend à entraîner les ions sur des trajectoires radiales décentrées (Figure 4).

La superposition de ce mouvement magnétron au mouvement cyclotronique se traduit par un abaissement de la fréquence cyclotronique observée. On définit alors la fréquence cyclotronique réduite, notée , ainsi que la fréquence magnétron, notée . Les expressions de ces deux fréquences sont données respectivement par les équations (6) et (7) (45).

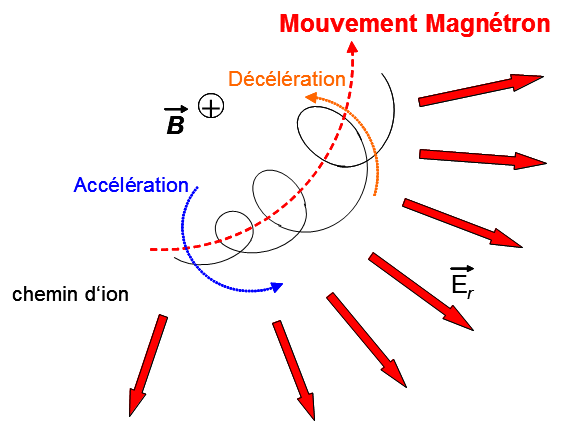
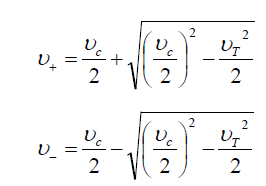
Malgré cet affaiblissement de la fréquence cyclotronique, une approximation est généralement adoptée en pratique, selon laquelle :

En effet, pour des ions de faible rapport , la fréquence cyclotronique réduite est très proche de la fréquence cyclotronique idéale . En revanche, pour des ions de rapport élevé, la fréquence cyclotronique diminue et l’influence de la fréquence de piégeage devient significative. Dans ce cas, l’écart entre et peut devenir non négligeable.

Afin de limiter cette différence entre la fréquence théorique et la fréquence effectivement observée, il est préférable d’appliquer un potentiel de piégeage faible, typiquement de l’ordre de 1 V.

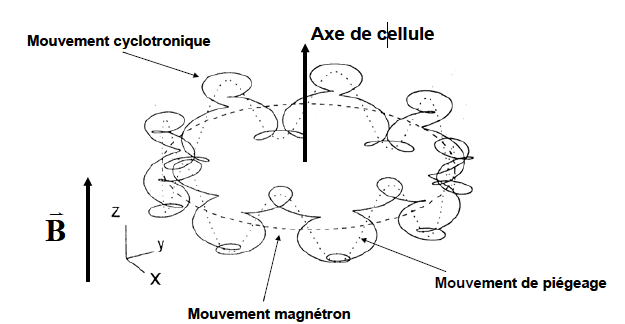
La combinaison des trois mouvements ioniques au sein de la cellule ICR à savoir le mouvement cyclotronique, le mouvement de piégeage axial et le mouvement magnétron est illustrée à la Figure 5. Parmi ces trois mouvements, le mouvement magnétron et le mouvement de piégeage présentent des fréquences nettement plus faibles que celle du mouvement cyclotronique. En règle générale, la fréquence de piégeage et la fréquence magnétron peuvent être négligées, sauf lorsque l’ion est décentré par rapport à l’axe du piège et/ou lorsque l’amplitude de son mouvement devient comparable à la distance séparant les parois de la cellule de piégeage .

trajectoire d'un ion dans la cellule ICR — Figure 5. Trajectoire d’ion dans la cellule ICR (45).

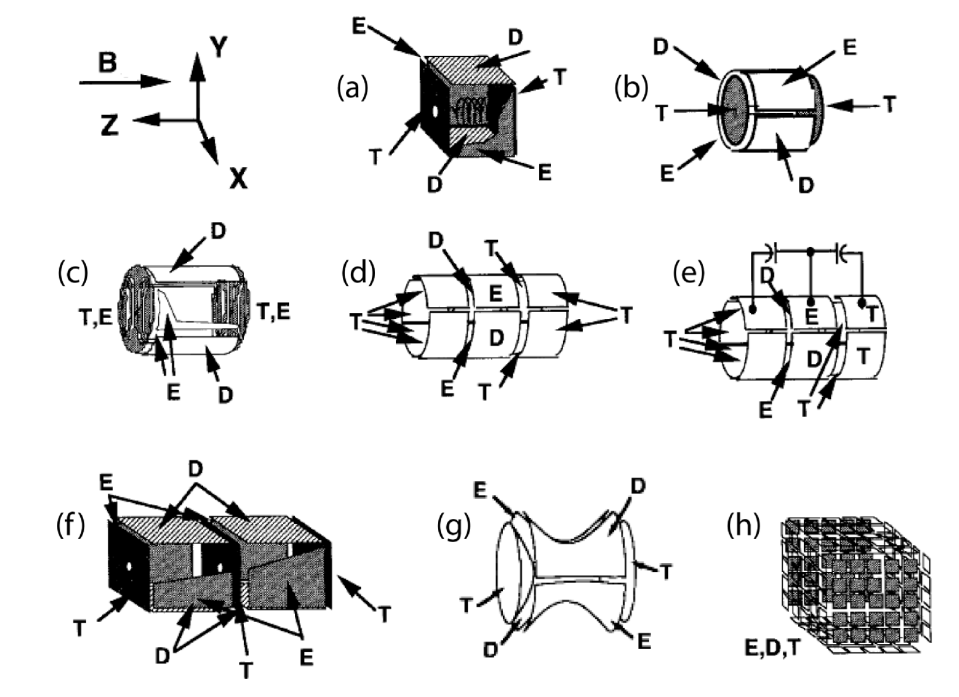
Différents types de cellules ICR ont été développés au fil du temps (Figure 6). Ces évolutions géométriques visent principalement à optimiser le confinement et le comportement dynamique des ions dans la cellule. Les objectifs recherchés sont notamment :
i) l’obtention d’un potentiel de piégeage générant un champ électrique radial aussi faible que possible,
ii) l’augmentation du diamètre effectif du piège, afin d’améliorer la capacité de stockage ionique, et
iii) une meilleure linéarité de l’excitation dipolaire, garantissant une excitation plus homogène des ions.

Différents type de cellules ICR — Figure 6. Différents types de cellule FT-ICR (modifiée à partir du schéma publié par Marshall), avec ses différents plaques : E = excitation, D = détection; T = piégeage. (a) cellule cubique initiale, (b) cellule cylindrique, (c) cellule cylindrique dite “Infinie”, (d) et (e) cellule cylindrique ouverte sans ou avec un couplage capacitif, (f) double cellule cubique, (g) cellule hyperboloïdale et (h) cellule “ matrix-shimmed”.

Principe de fonctionnement

L’enregistrement d’un spectre de masse FT-ICR repose sur la détection des courants induits par le mouvement cyclotronique des ions sur les plaques dites de détection. Toutefois, dans un premier temp

s, le signal cyclotronique n’est pas directement détectable. En effet, dans les instruments équipés d’une source d’ions externe, les ions de rapports différents sont introduits dans la cellule ICR avec des énergies cinétiques variables et à des instants distincts, en raison de leur temps de vol respectif.

Par conséquent, les ions sont déphasés les uns par rapport aux autres et décrivent initialement des orbites de faible rayon, ce qui empêche la génération d’un signal détectable. Il est donc nécessaire de faire évoluer une population d’ions de même rapport depuis un mouvement collectif incohérent caractérisé par des ions déphasés vers un mouvement collectif cohérent, dans lequel les ions oscillent en phase sur une orbite commune de plus grand rayon.

Pour atteindre cet état cohérent, une procédure d’excitation est appliquée préalablement à la détection. Cette étape d’excitation permet de synchroniser le mouvement des ions et constitue une condition indispensable à l’enregistrement du signal cyclotronique (Figure 7).

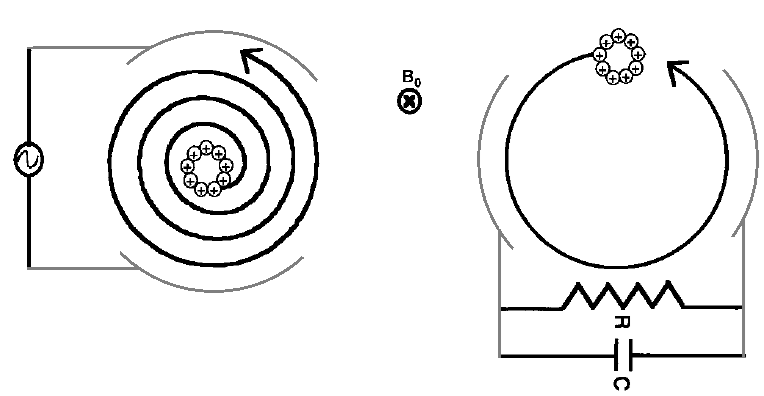
Excitation des ions dans une cellule ICR — Figure 7: Processus de fonctionnement de la cellule FT-ICR pour l’obtention de spectre de masse (modifiée à partir de (45)) : après excitation, les ions adoptent un mouvement cohérent ainsi qu’une orbite de rayon plus important permettant d’obtenir un signal mesurable sur les deux plaques de détection.

Excitation résonante des ions et cohérence du signal

Les méthodes classiques d’excitation résonante visent à synchroniser le mouvement cyclotronique des ions afin d’assurer la cohérence du signal détecté. Elles reposent sur l’application d’un champ radiofréquence adapté et peuvent être classées en deux grandes catégories.

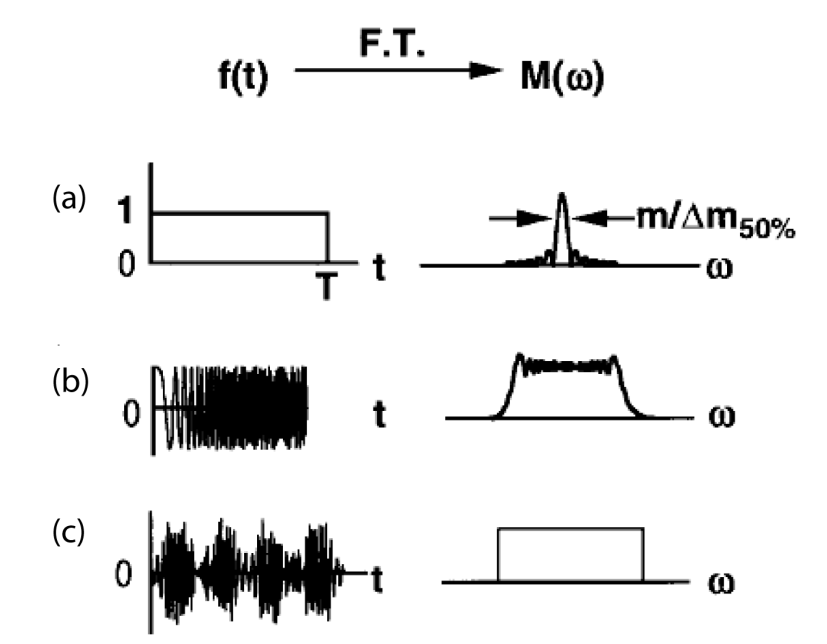
i) Excitation par impulsion rectangulaire

Cette méthode consiste à appliquer une impulsion radiofréquence de forme rectangulaire à une fréquence unique, correspondant à un ensemble d’ions de même rapport (Figure 8a). Elle permet une excitation sélective, mais reste limitée à une gamme étroite de masses.

ii) Excitation « broadband » (large bande)

Les méthodes d’excitation large bande permettent d’exciter simultanément des ions couvrant une large plage de rapports . Deux approches principales sont généralement employées :

Méthode dite « R.F. chirp » (Figure 8b)
Elle repose sur l’application d’une unique impulsion d’excitation dont la fréquence balaie continûment la plage de fréquences d’intérêt. Cette approche permet une excitation rapide et efficace d’un large ensemble d’ions.
Méthode « SWIFT » (Stored Waveform Inverse Fourier Transform) (Figure 8c)
Dans cette méthode, le domaine fréquentiel d’excitation est défini a priori. L’onde d’excitation correspondante est ensuite calculée par transformée de Fourier inverse, permettant une excitation sélective et contrôlée des ions tout en excluant certaines plages de masse si nécessaire.

méthodes d'exciation des ions — Figure 8 : Différentes méthodes d’excitation avec le domaine de temps à gauche et le domaine de fréquence à droite (modifiée à partir de schéma publié par Marshall(45)): (a) impulsion rectangulaire (mono-fréquence), et par un ensemble de fréquences appliquées pour différentes masse (b) R.F. chirp et, (c) SWIFT.

Dans le cas de l’excitation par impulsion rectangulaire (Figure 10a), un champ électrique dipolaire sinusoïdal est appliqué de manière homogène au sein de la cellule FT-ICR. La fréquence de ce champ correspond à la fréquence cyclotronique des ions possédant un rapport donné, ce qui permet de mettre ces ions en résonance et de conduire à un mouvement collectif cohérent caractérisé par une orbite de plus grand rayon.

Les ions présentant des rapports différents, et donc des fréquences cyclotroniques distinctes, ne sont pas en résonance avec la radiofréquence appliquée. Ils n’absorbent ainsi pas d’énergie et demeurent confinés au centre du piège. Afin de caractériser l’orbite décrite par un ensemble d’ions excités à leur fréquence cyclotronique, il est possible de calculer le rayon de l’orbite à partir de l’équation (8).

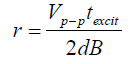
V_p-p: tension d’excitation (en V) ;

t_exit: durée de l’irradiation ; (en s) ;

d : distance entre les plaques d’excitation (en m) ;

A titre d’exemple : pour Vp-p= 1V, texcit = 0,2 ms, d= 2,54 cm et B= 7 Tesla. Le rayon d’excitation sera égal à 0,5 cm.

Il convient de noter que, selon cette équation, le rayon cyclotronique des ions après excitation est indépendant de leur rapport $m / z$ . Ainsi, tous les ions possédant le même rapport $m / z$ peuvent être excités jusqu’à un rayon identique. Théoriquement, plus le rayon de l’orbite est important, plus l’intensité du signal détecté est élevée. Néanmoins, cette orbite ne peut pas être excessivement grande, car l’inhomogénéité du champ électrique peut alors conduire à l’éjection des ions hors de la cellule. En pratique, le rayon de l’orbite $r$ doit rester inférieur à 0,4 fois la distance séparant les deux plaques d’excitation. Il est également important de souligner que ce type d’excitation, limité à un rapport $m / z$ unique, ne présente pas d’intérêt pour l’enregistrement d’un spectre de masse complet.

À l’inverse, l’excitation large bande est le plus souvent réalisée par la méthode dite « R.F. chirp » (dérive de fréquence) (Figure 10b) (82). Cette approche repose sur l’application d’une impulsion unique d’excitation, dont la fréquence balaie continûment la gamme de fréquences d’intérêt. Toutefois, les limites de ce mode d’excitation résident dans le manque d’uniformité de l’amplitude d’excitation, ce qui se traduit par une distorsion des abondances relatives des ions excités, ainsi que par une plage de rapports $m / z$ restreinte à celle couverte par la fréquence appliquée.

Afin de pallier ces limitations, la méthode « SWIFT » (Stored Waveform Inverse Fourier Transform) (83,84) (Figure 10c) a été développée. Cette approche repose sur une meilleure cohérence entre l’excitation et l’émission du signal dans la cellule FT-ICR, permettant une excitation plus homogène des ions. Une forme d’onde d’excitation spécifique est alors générée par transformée de Fourier inverse à partir d’un domaine fréquentiel prédéfini, incluant uniquement les fréquences de résonance des ions à exciter. Cette méthode permet ainsi l’analyse d’un ensemble d’ions couvrant une large gamme de rapports $m / z$ , tout en limitant les distorsions d’intensité.

Détection du signal

a) Origine du signal

Le mouvement cyclotronique cohérent d’un paquet d’ions de même rapport $m / z$ entre les deux plaques de détection induit un courant image mesurable (équation (9)) (85). Ce courant résulte du déplacement périodique des charges ioniques à proximité des électrodes de détection. Le signal ICR enregistré est directement proportionnel à la variation de charge induite, notée , et donc à l’amplitude du mouvement collectif des ions.

QΔ: courant induit par le paquet d’ions ;
yν: la vitesse dans l’axe y ;
d: distance entre les plaques d’excitation.

* : Dans cette description, seul l’axe est considéré. En réalité, le courant induit résulte de l’intégration des contributions selon les axes définis par les plaques de détection (Figure 9). Selon cette équation, le courant induit apparaît indépendant de la fréquence cyclotronique des ions ainsi que de l’intensité du champ magnétique. En revanche, il dépend du rayon cyclotronique des ions après excitation (équation (8)), puisque la vitesse ionique selon l’axe v_y est proportionnelle à ce rayon (équation (7)).

Par ailleurs, le courant induit augmente linéairement avec la charge des ions. Par conséquent, le signal ICR est d’autant plus intense pour des ions multichargés.

b) Nécessité d’un signal transitoire de longue durée

Au cours de l’acquisition du signal, plusieurs phénomènes peuvent altérer sa qualité. En particulier, la présence d’un gaz résiduel dans la cellule ICR entraîne des collisions ion–neutre. Ces collisions provoquent une perte d’énergie cinétique des ions, se traduisant par une diminution aléatoire du rayon cyclotronique ainsi que par une perte progressive de la cohérence de phase des ions de même rapport .

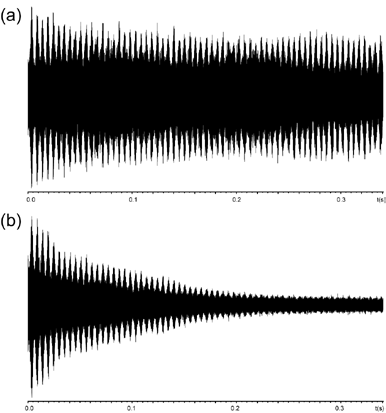
Le déphasage induit conduit à la génération de courants induits en opposition de phase, dont la somme peut devenir partiellement, voire totalement, nulle. Ce phénomène se manifeste par l’apparition de battements dans le signal. Les collisions ion–neutre sont ainsi responsables de l’atténuation du signal, qui suit une décroissance exponentielle caractéristique, communément appelée Free Induction Decay (FID).

Cette atténuation limite la durée exploitable du signal transitoire, ce qui entraîne une diminution du pouvoir résolutif de l’instrument FT-ICR (Figure 9). Il est donc primordial de travailler avec un nombre limité d’ions et sous un vide extrêmement poussé dans la cellule ICR, typiquement de l’ordre de 10^-10 mbar, afin de maximiser la durée du signal transitoire et les performances analytiques.

c) « Battement » du signal

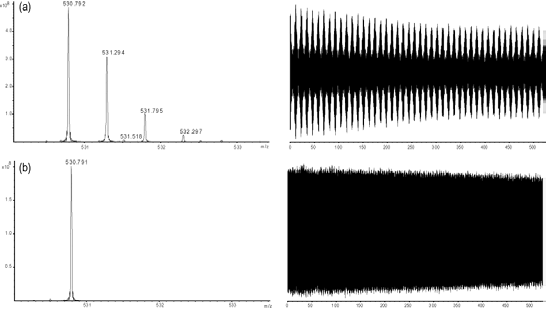
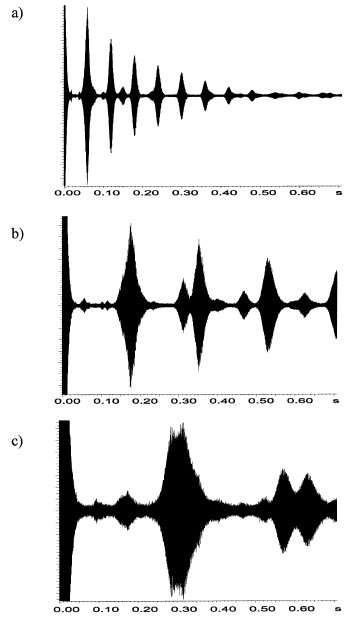
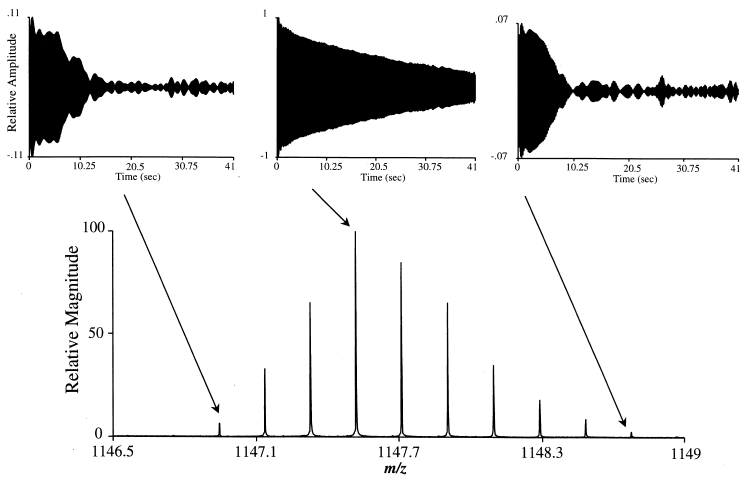
Lors de l’analyse d’espèces présentant un rapport élevé à l’aide d’un instrument FT-ICR, le signal transitoire obtenu peut présenter un motif de répétition périodique communément appelé « isotope beating » (Figure 10). Comme son nom l’indique, ce phénomène résulte des interférences constructives et destructives entre les signaux générés par les différents isotopes naturels d’un même ion, dont les fréquences cyclotroniques sont très proches. Cet effet est particulièrement marqué pour les ions multichargés, pour lesquels l’écart entre les fréquences cyclotroniques des isotopes naturels est encore plus faible (Figure 11). En conséquence, le signal résultant présente des modulations d’amplitude caractéristiques au cours du temps. La présence de ce phénomène impose l’acquisition d’un signal transitoire suffisamment long, afin de garantir que les différentes phases d’interférence soient correctement enregistrées et que le signal exploitable puisse être détecté avec une résolution optimale.

Figure 12 : Spectres de masse d’isolement de l’ion m/z 531 avec une fenêtre (a) de 5 Th, et (b) de 0.5 Th conduisant à la sélection de l’ion monoisotopique uniquement. — Figure 10 : Spectres de masse d’isolement de l’ion m/z 531 avec une fenêtre (a) de 5 Th, et (b) de 0.5 Th conduisant à la sélection de l’ion monoisotopique uniquement.

Figure 11 : Signal transitoire du domaine de temps (a) bovine insuline avec un état de charge +5 (Mw = 5729, m/z 1147 Da), (b) cytochrome c avec un état de charge +8 (Mw=12360, m/z 1544 Da) et (c) myoglobine avec un état de charge +10 (Mw = 17554, m/z 17544 Da), collecté avec un aimant de 7 Tesla (86).

d) Taux d’échantillonnage

Comme discuté précédemment, l’augmentation du pouvoir résolutif d’un instrument FT-ICR nécessite l’enregistrement d’un signal transitoire de longue durée. Pour un nombre de points d’acquisition donné, cette durée dépend directement de la mémoire du convertisseur analogique numérique (ADC) et du taux d’échantillonnage utilisé.

En mode de détection dit « large bande », le taux d’échantillonnage doit être suffisamment élevé pour respecter le critère de Nyquist (87), selon lequel la fréquence d’échantillonnage doit être au moins deux fois supérieure à la fréquence maximale du signal. Par exemple, pour détecter le signal induit par un ion de dans un champ magnétique de 7 T, correspondant à une fréquence cyclotronique kHz, un taux d’échantillonnage minimal de 430 kHz est requis. Dans ces conditions, l’utilisation d’un taux d’échantillonnage de 500 kHz permet l’enregistrement d’un signal transitoire d’une durée de 2 s, correspondant à un million de points acquis.

Afin d’enregistrer un signal transitoire de plus longue durée sans augmenter excessivement la taille des données, il est nécessaire de recourir au mode de détection hétérodyne (46,88), également appelé détection à bande étroite (narrow-band). Ce mode de détection permet l’utilisation d’un taux d’échantillonnage plus faible, tout en conservant une haute résolution.

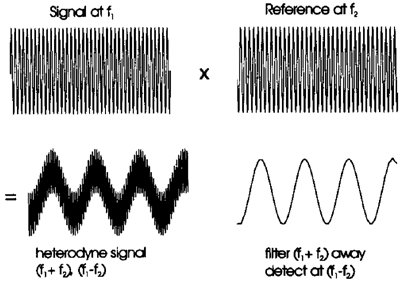
Dans la détection hétérodyne, le signal issu du courant induit de fréquence $f_1$ est multiplié par un signal de référence de fréquence $f_2$ , choisie proche de celle du signal d’intérêt. La combinaison de ces deux signaux sinusoïdaux génère un signal composite comportant deux composantes fréquentielles correspondant à la somme et à la différence des fréquences initiales, à savoir . La composante de haute fréquence est ensuite éliminée à l’aide d’un filtre passe-bas, ne conservant que la composante de basse fréquence.

Cette approche permet de réduire considérablement le taux d’échantillonnage requis, et donc d’augmenter la durée du signal transitoire enregistré, au prix toutefois d’une réduction de la gamme de rapports accessible simultanément. Le principe de la détection hétérodyne est illustré à la Figure 12.

Figure 12. Illustration du principe de détection “hétérodyne” (46).

e) La charge d’espace sur la qualité du spectre de masse

Comme dans l’ensemble des cellules de piégeage d’ions, la présence d’un nombre élevé d’ions de même polarité peut engendrer des répulsions ion–ion, communément désignées sous le terme de charge d’espace. Dans les pièges à ions de Paul, ces interactions conduisent à des déplacements apparents des rapports et à une dégradation de la résolution. De manière analogue, dans une cellule FT-ICR, lorsque le nombre d’ions piégés devient trop important, les interactions de répulsion entre ions doivent être prises en compte, car elles peuvent entraîner une modification des fréquences cyclotroniques.

L’amplitude de cet effet dépend notamment du rayon cyclotronique des ions. Afin d’obtenir une précision optimale en , il est donc nécessaire de procéder à l’étalonnage de l’instrument dans des conditions comparables, en particulier en termes de population ionique présente dans la cellule lors de l’analyse. Par ailleurs, lorsque la charge d’espace devient très élevée, des phénomènes dits de coalescence peuvent apparaître : des ions de rapports $m / z$ très proches ne sont alors plus résolus individuellement et se confondent en un signal unique.

Le nombre d’ions influence également la durée du signal transitoire. Il a été montré qu’une population ionique plus importante conduit à une atténuation plus lente du signal transitoire. Cette situation peut paradoxalement entraîner une réduction du pouvoir résolutif isotopique, rendant plus difficile la séparation d’ions isobares. En effet, dans certains cas notamment lors de l’enregistrement de signaux transitoires de longue durée une discrimination en faveur des isotopes de plus forte abondance peut apparaître (89,90).

Ainsi, comme illustré à la Figure 13, le signal transitoire associé aux ions de faible abondance isotopique présente une atténuation plus rapide que celui correspondant aux isotopes majoritaires, ce qui limite leur contribution effective au signal détecté.

Figure 13 : Extrait des signaux du domaine temporel pour les pics isotopiques individuels de l’état de charge 51 de l’insuline bovine (Mw 58548). Les différences dans l’amortissement du signal varient avec l’abondance des espèces isotopiques (89).

Afin d’améliorer la qualité du spectre de masse obtenu après la transformée de Fourier, différents traitements peuvent être appliqués au signal transitoire numérisé, notamment l’apodisation et le zero-filling.

L’apodisation consiste à multiplier le signal transitoire par une fonction de pondération, généralement sinusoïdale, afin de réduire les artéfacts spectraux observés au pied des pics du spectre de masse. Ces artéfacts proviennent de la troncation brutale du signal transitoire au début et à la fin de l’acquisition dans le domaine temporel. Les fonctions d’apodisation permettent de minimiser cet effet en forçant le signal transitoire à tendre progressivement vers zéro de manière monotone aux extrémités de l’acquisition. Toutefois, ce traitement s’accompagne d’une diminution du pouvoir résolutif, qui peut par exemple passer de 80 000 à 60 000.

Le traitement par zero-filling consiste à augmenter artificiellement le nombre de points du signal transitoire par ajout de zéros (doublement, triplement, etc.), ce qui permet de réduire l’intervalle de fréquence après transformée de Fourier. Bien que le zero-filling n’augmente pas la résolution réelle de l’instrument, il permet d’améliorer la définition des pics et de réduire les erreurs sur la hauteur et la largeur des signaux.

Par ailleurs, avant l’application de la transformée de Fourier, il est possible d’accumuler plusieurs signaux transitoires (FID) successifs. Cette accumulation conduit à une amélioration du rapport signal-sur-bruit, le signal augmentant linéairement avec le nombre d’accumulations, tandis que le bruit croît proportionnellement à la racine carrée de ce nombre.

Traitement du signal – Transformée de Fourier

Le signal ICR sinusoïdal, issu du mouvement cyclotronique périodique des ions, est tout d’abord amplifié, puis numérisé à l’aide d’un taux d’échantillonnage approprié. Conformément au critère de Nyquist (87), la fréquence d’échantillonnage d’un signal doit être au moins égale à deux fois la fréquence maximale contenue dans ce signal — cette fréquence maximale correspondant à celle de l’ion de plus faible rapport que l’on souhaite détecter. Cette condition est indispensable pour convertir correctement le signal d’une forme analogique continue vers une forme numérique discrète, sans perte d’information. La durée de détection du signal ionique, qui conditionne directement le pouvoir résolutif, dépend ainsi à la fois du plus petit rapport détecté et du nombre de points de données acquis. Ce nombre de points est limité par les capacités informatiques et se situe généralement entre un et deux millions de points dans les instruments FT-ICR actuels.

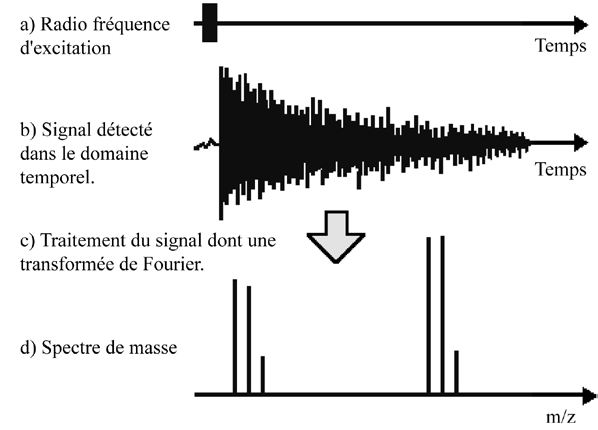
Le signal transitoire, initialement enregistré dans le domaine temporel, est ensuite converti dans le domaine fréquentiel par l’application d’une transformée de Fourier. Enfin, ce spectre de fréquences est transformé en un spectre de masse, reliant chaque fréquence cyclotronique à un rapport donné (Figure 14).

Figure 14 : Obtention et traitement du signal produit par des ions en mouvement cohérent au sein d’une cellule ICR : obtention d’un spectre de masse.

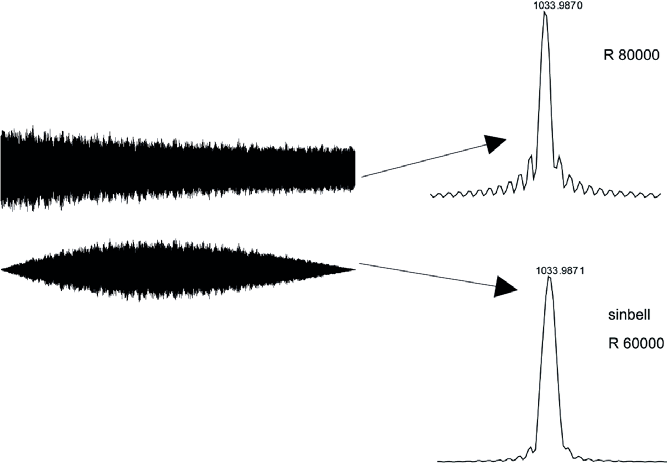
L’apodisation consiste à multiplier le signal transitoire par une fonction de pondération, généralement sinusoïdale, afin de réduire les artéfacts spectraux observés au pied des pics du spectre de masse. Ces artéfacts proviennent de la troncation brutale du signal transitoire au début et à la fin de l’acquisition dans le domaine temporel. Les fonctions d’apodisation permettent de minimiser cet effet en forçant le signal transitoire à tendre progressivement vers zéro de manière monotone aux extrémités de l’acquisition (Figure 15). Toutefois, ce traitement s’accompagne d’une diminution du pouvoir résolutif, qui peut par exemple passer de 80 000 à 60 000.

Le traitement par zero-filling (Figure 18) consiste à augmenter artificiellement le nombre de points du signal transitoire par ajout de zéros (doublement, triplement, etc.), ce qui permet de réduire l’intervalle de fréquence après transformée de Fourier. Bien que le zero-filling n’augmente pas la résolution réelle de l’instrument, il permet d’améliorer la définition des pics et de réduire les erreurs sur la hauteur et la largeur des signaux.

Figure 15 : Schéma du traitement par Apodisation, en haut signal avant le traitement, et en bas après le traitement.

la résolution du FT-ICR

Haut pouvoir résolutif et précision de masse

L’obtention d’un haut pouvoir résolutif en spectrométrie de masse FT-ICR repose sur la capacité à maintenir un signal transitoire cohérent sur une durée suffisamment longue, généralement de l’ordre de plusieurs secondes. Toutefois, la durée effective de ce signal est principalement limitée par les conditions expérimentales au sein de la cellule ICR, en particulier l’intensité du champ magnétique et la pression résiduelle.

Comme décrit précédemment, la présence de gaz résiduel dans la cellule peut entraîner des collisions ion–neutre avec les ions piégés. Ces collisions induisent une perte de cohérence de phase, réduisant ainsi la durée pendant laquelle les ions restent cohérents entre eux. Même une faible augmentation de la pression conduit à une diminution notable de la durée du signal transitoire. À l’inverse, lorsque la pression est suffisamment faible, typiquement de l’ordre de 10^-10mbar, la largeur des pics dans le spectre de fréquences n’est plus uniquement gouvernée par les phénomènes de collision.

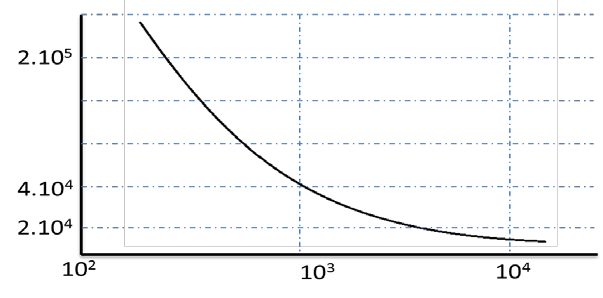
Dans ces conditions, la fréquence cyclotronique étant inversement proportionnelle au rapport , les pics spectraux deviennent de plus en plus proches lorsque le rapport augmente. Il en résulte une diminution du pouvoir résolutif, défini comme à 50 % de hauteur, pour les ions de rapport (Figure 16).

Figure 16. Evolution de la résolution en fonction de m/z.

Un haut pouvoir résolutif constitue un élément essentiel pour atteindre une précision élevée de mesure de masse. Toutefois, il ne s’agit pas du seul critère garantissant la précision des mesures en spectrométrie FT-ICR (92). Il est en effet indispensable de procéder à un étalonnage précis des rapports $m / z$ . La qualité de cet étalonnage est fortement influencée par les effets de charge d’espace au sein de la cellule ICR.

Lorsque la densité d’ions devient importante, des forces de répulsion ion–ion apparaissent du fait de la faible distance séparant les espèces chargées. Ces interactions modifient légèrement les trajectoires ioniques, ce qui se traduit par un déplacement des pics observés dans le spectre de masse. Dans des conditions optimales, l’étalonnage interne permet d’atteindre une précision en inférieure à 1 ppm, puisque l’étalon interne est détecté dans les mêmes conditions expérimentales que les ions analytes. Cette approche permet ainsi de compenser partiellement les effets de charge d’espace, bien que ceux-ci ne soient pas totalement supprimés.

Néanmoins, dans certains cas, l’étalonnage interne s’avère difficile à mettre en œuvre, notamment lors de certaines expériences MS/MS, où les ions fragments ne sont pas identifiés a priori. Il est alors nécessaire de recourir à un étalonnage externe. Dans ce contexte, la précision des mesures dépend étroitement du nombre d’ions piégés dans la cellule ICR. Il est donc préférable de travailler avec une population ionique aussi faible que possible, afin de minimiser les effets de charge d’espace et d’améliorer la précision des rapports . En pratique, l’étalonnage externe permet d’atteindre une précision de l’ordre du ppm, à condition que le spectre de masse soit enregistré dans des conditions expérimentales comparables (pression, nombre d’ions, etc.).

Il convient enfin de souligner que certains instruments hybrides, tels que les systèmes combinant un piège à ions linéaire et une cellule FT-ICR, permettent une mesure préalable du courant ionique dans le piège à ions. Cette étape autorise l’introduction d’un nombre d’ions contrôlé et constant dans la cellule ICR, contribuant ainsi à une amélioration significative de la précision des mesures de lors d’un étalonnage externe.

Inconvénients et limitations du FT-ICR

Malgré ses performances analytiques exceptionnelles, la spectrométrie de masse FT-ICR présente également plusieurs limitations. Tout d’abord, il s’agit d’un instrument technologiquement complexe et sophistiqué, dont l’utilisation requiert une expertise spécifique. De ce fait, le FT-ICR n’est généralement pas recommandé pour des analyses de routine.

L’une des principales limitations du FT-ICR réside dans son coût très élevé, tant à l’achat qu’à l’entretien. En effet, l’obtention d’un champ magnétique très intense nécessite l’utilisation d’aimants supraconducteurs, lesquels doivent être maintenus à des températures extrêmement basses, proches du zéro absolu. Ce refroidissement est assuré par de l’hélium liquide, lui-même thermiquement isolé de l’environnement extérieur par une couche d’azote liquide. Ces deux fluides cryogéniques doivent être rechargés régulièrement, ce qui contribue significativement aux coûts d’exploitation et aux contraintes logistiques.

Par ailleurs, afin d’atteindre une très haute résolution, l’enregistrement du signal transitoire doit être relativement long. Cette contrainte se traduit par une réduction de la vitesse d’acquisition, limitant le débit d’analyse par rapport à d’autres technologies de spectrométrie de masse. Enfin, les analyses réalisées en FT-ICR génèrent des fichiers de données volumineux, en raison de la durée d’acquisition et du nombre élevé de points enregistrés, ce qui implique des besoins importants en capacité de stockage et en puissance de calcul.

Référence

[1] Marshall A.G., Hendrickson C.L., Jackson G.S.. Fourier transform ion cyclotron resonance mass spectrometry: a primer. Mass Spectrom. Rev. 1998, 17, 1.

[2] Amster I.J.. Fourier transform mass spectrometry. J. Mass Spectrom. 1996, 31, 1325.

[3] Vartanian V.H., Anderson J.S., Laude D.A.. Advances in trapped ion cells for fourier transform ion cyclotron resonance mass spectrometry. Mass Spectrom. Rev. 1995, 14, 1.

[4] Lawrence E.O. and Edlefsen N.E.. On the production of high speed proton. Science. 1930, 72, 376.

[6] Hipple J.A., Sommer H., Thomas H.A.. A precise method of determining the faraday by magnetic resonance. Phys. Rev. 1949, 76, 1877

[7] Sommer H., Thomas H.A., Hipple J.A.. The measurement of e/M by cyclotron resonance. Phys. Rev. 1951, 82, 697

[8] Wobschall D. Ion cyclotron resonance spectrometer. Rev. Sci. Instrum. 1965, 36, 466.

[9] McIver R.T. Jr.. Trapped ion analyzer cell for ion cyclotron resonance spectroscopy. Rev. Sci. Instrum. 1970, 41, 555.

[10] Comisarow M.B., Marshall A.G. Fourier transform ion cyclotron resonance spectroscopy. Chem. Phys. Lett. 1974, 25, 282.

[11] Henry K.D., Williams E.R., Wang B.H., McLafferty F.W., Shabanowitz J., Hunt D.F. Fourier-transform mass spectrometry of large molecules by electrospray ionization. Proc. Natl. Acad . Sci. USA. 1989, 86, 9075.

[12] Castro J.A., Koster C., Wilkins C.. Matrix-assisted laser desorption/ionization of high-mass molecules by Fourier-transform mass spectrometry. Rapid comm. mass spectrom. 1992, 6, 239.

[13] Riegner D.E., Laude D.A., Jr.. Collision-mediated axial ejection of radially excited ions as a mass-dependent ion loss mechanism in Fourier transform ion cyclotron resonance mass spectrometry. Int. J. Mass Spectrom. Ion Proc. 1992, 120, 103.

[14] Brown S.C., Kruppa G., Dasseux J.L.. Metabolomics applications of FT-ICR mass spectrometry. Mass Spectrom. Rev. 2005, 24, 223.

[15] Ghaderi S., Kulkarni P.S., Ledford E. B., Jr., Wilkins C.L., Gross M.L.. Chemical ionization in Fourier transform mass spectrometry. Anal. Chem. 1981, 53, 428.

[16] Comisarow M.B., Melka J.D. Error estimates for finite zero-filling in Fourier transform spectrometry. Anal. Chem. 1979, 51, 2198.

[17] Aarstol M., Comisarow M.B.. Apodization of FT-ICR spectra. Int. J. Mass Spectrom. Ion Proc. 1987, 76, 287.

[18] Guan S., Marshall A.G.. Ion traps for Fourier transform ion cyclotron resonance mass spectrometry: principles and design of geometric and electric configurations. Int. J. Mass Spectrom. Ion Proc. 1995, 146/147, 261.

[19] Marshall A.G., Guan S.H.. Advantages of high magnetic field for fourier transform ion cyclotron resonance mass spectrometry. Rapid Commun. Mass Spectrom. 1996, 10, 1819.

[20] Senko M.W., Hendrickson C.L., Emmett M.R., Shi S.D.H., Marshall A.G.. External accumulation of ions for enhanced electrospray ionization fourier transform ion cyclotron resonance mass spectrometry. J. Am. Soc. Mass Spectrom. 1997, 8, 970.

[21] Belov M.E., Nikolaev E.N., Anderson G.A., Auberry K.J., Harkewicz R., Smith R.D.. Electrospray ionization-Fourier transform ion cyclotron mass spectrometry using ion preselection and external accumulation for ultrahigh sensitivity. J. Am. Soc. Mass Spectrom. 2001, 12, 38.

[22] Senko M.W., Speir J.P., Mclafferty F.W.. Collisional activation of large multiply-charged ions using Fourier-transform mass-spectrometry. Anal. Chem. 1994, 66, 2801.

[23] Kellersberger K.A., Yu E., Kruppa G.H., Young M.M., Fabris D.. Top-Down characterization of nucleic acids modified by structural probes using high-resolution tandem mass spectrometry and automated data interpretation. Anal. Chem. 2004, 76, 2438.

[24] Little D.P., Speir J.P., Senko M.W., O’Connor P.B., McLafferty F.W.. Infrared multiphoton dissociation of large multiply charged ions for biomolecules sequencing. Anal. Chem. 1994, 66, 2809.

[25] Little D.P., Aaserud D.J., Valaskovic G.A., McLafferty F.W.. Sequence information from 42–108-mer DNAs (complete for a 50 mer) by tandem mass spectrometry. J. Am. Chem. Soc. 1996, 118, 9352.

[26] Cooper H.J., Hakansson K., Marshall A.G.. The role of electron capture dissociation in biomolecular analysis. Mass Spectrom. Rev. 2005, 24, 201.

[27] Yang J., Hakansson K.. Fragmentation of oligoribonucleotides from gas-phase ion-electron reactions. J. Am. Soc. Mass Spectrom. 2006, 17, 1369.